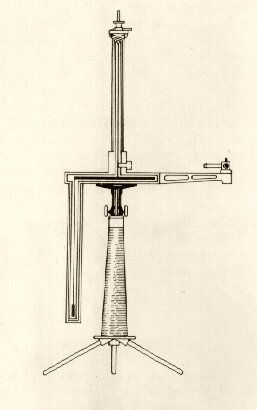
1. ábra A torziós inga rajza
Ephraim Fischbach
Purdue Egyetem,
Bod László, Nárayné Ziegler
Mária
KFKI,
Marx György
ELTE Atomfizikai Tanszéke
"Ars longa, vita brevis"
Eötvös Loránd a newtoni rendszer szépségétől indíttatva 1889-ben úgy határozott, hogy újra megvizsgálja kísérletileg a tehetetlen és a gravitációs tömeg arányosságát. Eredményeit, melyek a Bessel-féle 1/60 000-es pontosságot 1/20 000 000-ra javították egy rövid, három-oldalas közleményben jelentette meg a Magyar Tudományos Akadémia folyóiratában 1890-ben[1]. Ez az eredmény a Göttingeni Királyi Tudományos Társaság érdeklődését annyira felkeltette, hogy az 1906 évi Beneke-díj pályázatot a következő feltételekkel írták ki:
"Eötvös egy igen érzékeny módszert adott meg az anyag tehetetlenségének és gravitációjának az összehasonlítására. Erre való tekintettel figyelembe véve az elektrodinamika legújabb fejlődését is, valamint a radioaktív anyagok felfedezését, felmerül a tehetetlenség és a gravitáció arányosságára vonatkozó newtoni törvény meglehetősen széleskörű vizsgálatának a szükségessége."
A pályázatban foglaltaknak megfelelően Eötvös munkatársaival, Pekár Dezsővel és Fekete Jenővel 1906-ban egy méréssorozatot indított el, melynek keretében 1909-ig mintegy 4000 órányi mérés adatait gyűjtötték össze. A 16. Nemzetközi Geodéziai Konferencián, Londonban, 1909-ben Eötvös személyesen számolt be eredményeiről[2], a mérések során elért pontosságot 1/100 000 000 értékűnek adva meg. A teljes munkát Eötvös, Pekár és Fekete 1909-ben benyújtotta a Beneke Alapítványhoz. A díjat elnyerték. Jeligéjük "Ars longa, vita brevis" volt ("A művészet marad, az élet szalad"), ami tragikusan jellemzi Eötvös ezen munkájának a sorsát is[3]. A pályázat kiértékelésében C. Runge, a göttingai egyetem bölcsészeti fakultásának dékánja ezt írja[4]: annak ellenére, hogy Eötvösék dolgozatuk szerint 1/200 000 000-es pontosságot értek el, a Testület csak egy csökkentett összegű díj (3400 német márka 4500 helyett) odaítélését javasolja, mivel a benyújtott anyag nem tartalmazza a megfigyelt adatok igazi elméleti diszkusszióját.
Nem sokkal ezután kitört az első világháború,1919-ben meghalt Eötvös Loránd. Az 1906-1909 között elvégzett mérések részletes leírását munkatársai, Pekár és Fekete csak 1922-ben publikálták[5]. Ez az a dolgozat, melyet széles körben ismer és idéz a nemzetközi tudományos világ. Mikor 1953-ban az MTA felkérésére Selényi Pál, Eötvös tanítványa összeállította Eötvös műveinek gyűjteményes kiadását, az itt tárgyalt Eötvös-Pekár-Fekete-tanulmányhoz zárójelben helyenként kiegészítéseket fűzött, melyeket az eredeti kéziratból vett át[6]. Sajnos, ennek az eredeti kéziratnak azóta nyoma veszett.
A harmincas években az Eötvös-kísérletet
megismételte Renner János, aki szintén Eötvösnél
tanult. Eredményeit a Matematikai és Természettudományi
Értesítőben publikálta[7], szerinte
az elért kísérleti pontosság 1/2 000 000 000
és 1/5 000 000 000 között volt.
Dicke kritikai észrevételei
Felismerve a tehetetlen és gravitáló
tömeg viszonyának jelentőségét
az általános relativitás elméletben
Roll, Krotkov és Dicke új kísérletet
végzett el, ebben a modern technika alkalmazásával
1/100 000 000 000 pontosságot sikerült
elérniök a tehetetlen és gravitációs
tömeg arányosságát bizonyítva[8]. Dickéék azért is tudták a mérés
érzékenységét fokozni, mert a próbatömegnek
a Naphoz viszonyított gyorsulását mérték,
szemben Eötvössel, aki a Földhöz viszonyított
gyorsulással dolgozott. Ilyen kísérletekben
a két tömeg (a tehetetlen és a gravitáló)
különbözőségéből eredő
jelnek 24 órás periódicitást kellene
mutatnia a Föld tengely körüli forgási idejének
megfelelően. Ezáltal könnyen, a torziós
szál megzavarása nélkül kiszűrhetők
a zavaró háttérzajok, melyek nem ezt a periódicitást
mutatják. De természetesen igen nagy figyelmet kell
fordítani más, szintén 24 órás
periódussal jelentkező perturbációkra.
Tény marad, hogy Eötvös, Pekár és
Fekete voltak az elsők, akik összehasonlították
különböző anyagok Naphoz viszonyított
gyorsulását, és platina és mangán
esetén a frakcionális gyorsulás különbségre
6 10-9 értéket
adtak meg. Nem közölték azonban a mérési
hibát, az elvégzett vizsgálatot igen szűkszavúan
írták le, ezért nagyon nehezen mondható
meg, hogy kísérletük ezen részének
a pontossága miként viszonyul ahhoz a kiterjedtebb
vizsgálódáshoz, mikor az anyagnak a Földhöz
viszonyított gyorsulását mérték.

1. ábra A torziós
inga rajza
Eötvös eredményeit elemezve Dicke kétségeinek ad hangot, hogy vajon Eötvös asszisztensei ténylegesen elérték-e a célul kitűzött pontosságot. Gondolatmenetének főbb lépései a következők:
Vajon figyelembe vették-e a kísérlet elvégzése során a hőmérséklet-különbségek következtében esetleg fellépő légmozgás okozta perturbációt. Szerintünk Eötvös és munkatársai ebből a szempontból igen gondosan jártak el. A kísérletet egy jól árnyékolt, zárt szobában felállított dupla falú sátorban (a sátor két fala között afrik tömítéssel) végezték el. Maga a torziós inga (rajza az 1. ábrán látható) hármas falú, levegő szigetelésű réz tartóban volt. Hogy Eötvösék igencsak odafigyeltek a termikus effektusokra, még abból is kitűnik, hogy a torziós inga különböző helyeire hőmérőket szereltek fel. (A harmadik kísérletükben például, amikor már a kettős karú ingát használták, három hőmérőt helyeztek el: egyet-egyet a két karon és egyet a torziós szál közelében.) Dicke a feltételezett termikus effektusokkal óhajtotta megmagyarázni az Eötvös-adatokban fellépő, Fischbach által egy lehetséges Ötödik Erőnek tulajdonított korrelációkat. Ezért a kérdést később Fischbach és munkatársai részletesen megvizsgálták[10] s legfőbb ellenérvük Dicke kritikájával szemben az volt, hogy a feltételezett termikus effektusoknak a méréssorozat teljes ideje alatt azonos előjellel és azonos nagyságrendben kellett volna fellépniök. Figyelembe véve, hogy a méréssorozat több éven át tartott s mintegy 4000 órát tett ki, ez teljességgel elképzelhetetlen.
A mérést végző személy teste is okozhat nem kielégítően meghatározott gravitációs perturbációt. Ez a hibalehetőség Eötvös előtt is ismert volt. Épp ezért a megfigyelő nem tartózkodott a helyiségben, amíg a torziós inga lengésben volt. Módszerük a következő volt: mikor az inga nyugalomba került, a megfigyelő befutott a szobába, leolvasta a műszert, és újra elhagyta a helyiséget, mielőtt az inga újra kitért volna. (Az inga periódus ideje 40 perc volt[11].)
Sajnos mindezidáig nem sikerült teljes egészében rekonstruálni, hogy Eötvös, Pekár és Fekete miként végezte el mérési adataik statisztikus kiértékelését. (Erre vonatkozóan egyik publikációjukban sem adnak részletes információt.) Az MTA levéltárában őrzött Eötvös-hagyatékban fellelhető ugyan néhány mérési adatlap (egy ilyen látható a 2. ábrán), de ezek sem tartalmaznak elegendő információt a kiértékelés megismétléséhez. Ebben a vonatkozásban leginkább Renner 1935-ben megjelent cikkére támaszkodhatunk[7]. Innen látható, miként azt Dicke hangsúlyozta, hogy Renner a környezeti változások hatását időbeli interpolációval igyekezett kiküszöbölni. Az ilymódon nyert számértékek azonban statisztikusan nem függetlenek egymástól, de Renner mégis akként kezelte azokat. Így Dicke szerint a statisztikus hiba háromszorosa a Renner által megadottnak. Meg kell jegyeznünk, hogy később Király Péter is elvégezte ezeket a számításokat, ő a Renner által megadott hiba 2,4-szeresét kapta[12].
Ha ezt a megnövelt hibaforrást figyelembe vesszük, Renner által a kétféle tömeg eltérésére kapott érték gyanúsan közeledik a nullához. Ezen az alapon Dicke és munkatársai azt sugalmazzák, hogy a Renner féle eredményeket nem lehet komolyan venni. És tovább menve arra céloznak, hogy Renner kiértékelési technikáját minden bizonnyal Eötvöstől tanulta. Az Eötvös halála után Pekár által az Annalen der Physikhez eljuttatott tanulmányban[5] megadott hiba oka részben mérési, részben pedig kiértékelési pontatlanság lehet, de hogy e kettőből milyen arányban tevődik össze, sajnos nem tudjuk. Meglehet, hogy a valódi helyzetet az Eötvös által személyesen megadott 10-8-os pontosság jobban tükrözi. Ez is mindenképpen egy tiszteletre méltó teljesítmény. Az a meglepő tendencia pedig, amit Fischbachék vettek észre fennmaradni látszik. (Lásd a következő fejezetet.)

2. ábra
Adatlap az Eötvös hagyatékból
Végezetül szeretnénk hangsúlyozni, hogy mind Dicke, mind Fischbach elemzése szerint az Eötvös, Pekár, Fekete cikkben adott hibaértékek konzisztensek a közölt adatok statisztikus szórásával. Továbbmenve, Fischbach és társai által ezen adatokhoz elvégzett legjobb illesztés konfidenciaszintje 86 %, ilymódon elfogadható marad az Ötödik Erő létezésének sugalmazása is. Nyomaték kedvéért álljanak itt magának Eötvösnek a szavai:
Ennek a régi mondásnak intelme késztette
arra e dolgozat szerzőit, hogy vizsgálataik eredményét
összefoglalják és elbírálásra
egy magas, tudományos aeropag (törvényszék)
elé terjesszék. A vizsgálati módszerek
természetesen egyre finomodnak, javulnak a vizsgálat
folyamán és így egyetlen halandó sem
készülne el a munkájával, ha nem szabna
gátat annak a különben dicséretreméltó
törekvésnek, hogy a hasznavehetőt állandóan
a még jobbal váltsa fel. (Részlet a Pályamű
előszavából).
Az Ötödik Erő hipotézise
Méltán mondhatjuk, hogy az Eötvös-kísérlet a klasszikus fizika nagy évszázadának utolsó gyöngyszeme. Vizsgálataik végén Eötvös, Pekár és Fekete a tehetetlen és gravitációs tömeg arányosságát radioaktív anyagok esetén tanulmányozták[5]. (Ekkor az E = mc2 összefüggés már ismert volt.) Az arányosságot 0,l g RaBr2 minta esetén 1/2 000 000 pontossággal igazolták. A következő évtizedekben az anyag szerkezetének a vizsgálata a hosszú hatótávolságú gravitáción és elektromosságon, valamint a rövid-hatótávolságú mag- és gyönge-kölcsönhatásokon kívül más lehetséges természeti erőkre is felhívta a figyelmet. A kvantumelmélet szerint az erő r hatótávolsága r = h / mc szerint függ a hatást továbbító mező kvantumainak m tömegétől (h a Planck állandó és c a fénysebesség). A gravitációs és az elektromos mező erővonalainak végtelen hosszúsága logikailag összefügg a tömeg (energia) és töltés abszolút megmaradása törvényével. Amennyiben további egzakt vagy közelítő megmaradási törvények is léteznek (például a barion töltés megmaradása, melyet Wigner[13] fedezett fel), akkor fennáll annak a lehetősége, hogy egy további ismeretlen mező is létezik, amely egy Ötödik Erőt közvetíthet. Ha azonban e mező kvantumának nyugalmi tömege pontosan zérus lenne (mint a fotonok esetében), a forró testek ezeket a kvantumokat is sugároznák, ami ellentmondana a termodinamikai tapasztalatoknak. Ha viszont a kvantumoknak kicsi, de el nem tűnő tömeget tulajdonítunk, úgy az általuk transzmittált Ötödik Erőnek hosszú, de véges x0 = h / mc hatótávolságúnak kellene lennie. Ezzel a feltételezéssel tulajdonképpen két tömeg között azok összetételétől függő távolbahatást hívtunk életre. Így a hosszútávú kölcsönhatási energia a gravitáció és az ötödik erő okozta járulékok összege volna:
itt B ill. B' a kölcsönhatásban szereplő két tömeg barionszámát (a két testet alkotó protonok és neutronok számának összegét) jelöli. Csillagászati távolságoknál csak a newtoni gravitáció érvényesül, azaz
Laboratóriumi méreteknél azonban egy ettől eltérő "effektív tömegvonzás" volna megfigyelhető, azaz
ahol Geff az effektív gravitációs állandó, azaz
ami nem feltétlenül azonos a newtoni (csillagászati) G gravitációs állandóval. A fenti képletet átrendezve és bevezetve az M = m / mH kifejezést, ahol mH a hidrogén atom tömege, azt kapjuk, hogy
ahol a = F/Gm2H.
Itt B/M értéke hidrogénre 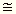 1, szénre
1,00782, rézre 1,00895 és ólomra 1,00794.
Ezek szerint az effektív gravitációs állandó
laboratóriumi körülmények között
mérve függhet az anyagi összetételtől.
1, szénre
1,00782, rézre 1,00895 és ólomra 1,00794.
Ezek szerint az effektív gravitációs állandó
laboratóriumi körülmények között
mérve függhet az anyagi összetételtől.
Az itt bemutatott hipotézis tapasztalati
ellenőrzését szolgálhatja a csillagászati
és laboratóriumi körülmények között
mért G értékek összehasonlítása,
ezenfelül az effektív gravitációs állandó
anyagi összetételtől való esetleges
függésének a mérése is. Eötvös
kísérleti eredményei mindkét irány
tisztázásához hozzájárultak.
Az eredményeket összefoglalóan a 3. ábra
szemlélteti, amelyet Király Péter[12]
állított össze.
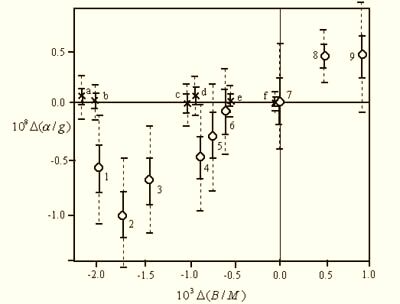
3. ábra Eötvösék (1-9) és Renner (a-f) által mért
/g értékek
(B/M) függvényében. A szaggatott vonalak a 2,4-szeresre növelt szórásnak felelnek meg. Összehasonlított anyagok az EPF mérésben: 1. faggyú - Cu; 2. víz - Cu; 3. CuSO4 oldat - Cu; 4. CuSO4 kristályok - Cu; 5. azbeszt - Cu; 6. fa - Pt; 7. ezüstszulfát + vasszulfát (reakció előtt és után); 8. magnalium - Pt; 9. Cu - Pt. Renner méréseiben: a) paraffin - sárgaréz; b) NH4F - Cu; c) Bi - sárgaréz; d) Pt - sárgaréz; e) üveg - sárgaréz; f) mangán-réz ötvözet - Cu.
Ezen az ábrán
különböző anyagpárokra van feltüntetve a mért
nehézségi gyorsulások
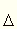
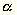 különbsége (osztva a g nehézségi gyorsulással). Mivel a nehézségi gyorsulás
a Föld vonzásából adódó gravitációs gyorsulás és a Föld forgásából adódó
inerciális gyorsulás eredője, iránya függ a gravitációs és tehetetlen
tömeg arányától. Eötvösék adatai Fischbach és munkatársai szerint B/M
függvényében lineáris függést mutatnak[9],
és az adott mérési pontoknak megfelelő
egyenes meredeksége 5,67 ± 0,7 • 10-6,
ami azt jelenti, hogy az a várt zérus értéktől
a szórás néhányszorosával eltér.
Mint a 3. ábrából látható, Renner adatai nem mutatnak szisztematikus függést
B/M-től.
Ha az Ötödik Erő tényleg létezik
és hatótávolsága - mondjuk - 100 m,
akkor az összetétel-függőség a
környezetben levő testek hatásának tulajdonítható.
különbsége (osztva a g nehézségi gyorsulással). Mivel a nehézségi gyorsulás
a Föld vonzásából adódó gravitációs gyorsulás és a Föld forgásából adódó
inerciális gyorsulás eredője, iránya függ a gravitációs és tehetetlen
tömeg arányától. Eötvösék adatai Fischbach és munkatársai szerint B/M
függvényében lineáris függést mutatnak[9],
és az adott mérési pontoknak megfelelő
egyenes meredeksége 5,67 ± 0,7 • 10-6,
ami azt jelenti, hogy az a várt zérus értéktől
a szórás néhányszorosával eltér.
Mint a 3. ábrából látható, Renner adatai nem mutatnak szisztematikus függést
B/M-től.
Ha az Ötödik Erő tényleg létezik
és hatótávolsága - mondjuk - 100 m,
akkor az összetétel-függőség a
környezetben levő testek hatásának tulajdonítható.
Az Ötödik Erő hipotézisnek
kettős hatása volt: számos modern kísérlet
elvégzését inspirálta, másrészt
megnövelte az érdeklődést az eredeti
Eötvös-Pekár-Fekete kísérlet és
a Renner-kísérlet körülményei iránt.
Jelen írásunkkal nem kívánunk csatlakozni
az Ötödik Erőhöz kapcsolódó
vitákhoz (ezekről az olvasónak bőven
volt lehetősége tájékozódni
a Fizikai Szemlében és a vonatkozó további
irodalomban[14,15],
csupán összegezni szeretnénk azokat az információkat,
amelyek a két klasszikusnak tekinthető magyar fizikai
kísérlettel kapcsolatban jelenleg hozzáférhetőek.
Mielőtt tovább mennénk, szeretnénk
az olvasók figyelmébe ajánlani néhány
sort, amit Nieto, Goldman és Hughes[16] írtak az
Eötvös kísérletről: "...abban
az időben még sem a barionszám fogalma,
sem a tömegdefektus fogalma nem létezett. Ezek nélkül
pedig Eötvösnek jelentős időt és
erőfeszítést kellett fordítania arra
az eredménytelen törekvésre, hogy kitalálja:
mérési adatainak a szórása vajon miért
nagyobb a becsült hibánál. Őszintén
együtt érezhetünk vele, elképzelhetjük
azt a mardosó érzést, hogy valamit rosszul
csináltak-e, vagy pedig valami igazán fontosat nem
vettek észre."
Látogatás Eötvös laboratóriumában
A Budapestet átszelő Duna geológiai törésvonal mentén folyik. Nyugati partját meredek mészkő- és dolomithegyek (CaCO3, MgCO3) szegélyezik. Keleti partja pedig teljesen sík, talaja leginkább nedves homok, amit a folyam rakott le. A terület legjellegzetesebb geológiai tulajdonsága tehát a kelet-nyugati aszimmetria (4. ábra). A Magyar Királyi Tudományegyetem, ahol Eötvös a kísérleteit végezte, a keleti parton található. A Fizikai Intézet épületét (ma Puskin utca 5) az 1880-as években maga Eötvös tervezte és építtette. Laboratóriuma helyén most az Atomfizikai Tanszék neutron-laboratóriuma van.
4. ábra A
Gellért hegy és az Eötvös egyetem közötti
terület geológiai térképe
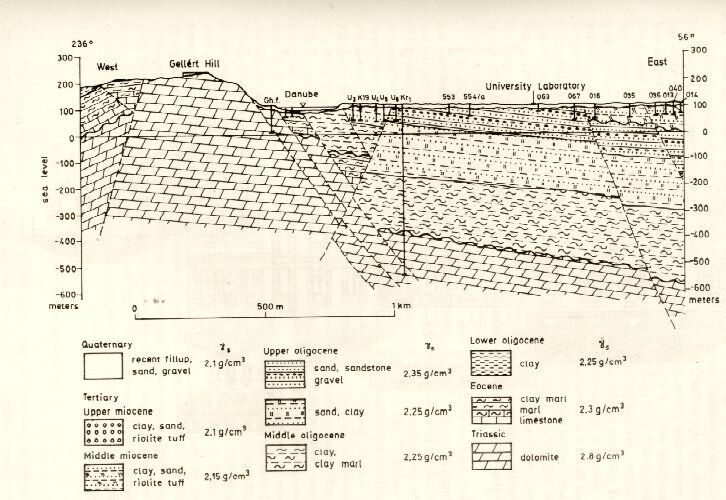
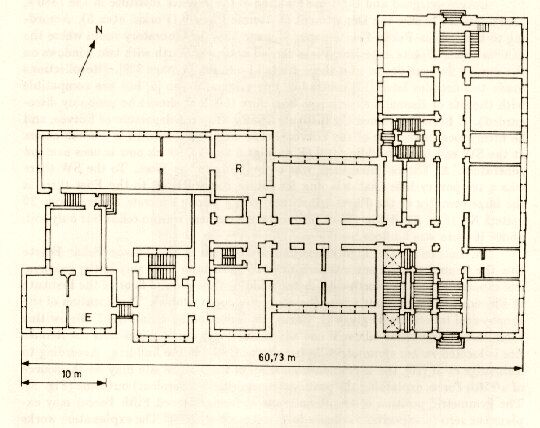
Az Eötvös-Pekár-Fekete-tanulmány szerint a laboratóriumnak, ahol a kísérletet elvégezték, a földszinten két délre néző ablaka volt, vele szemben pedig magas épületek álltak. Pekár Dezső két évtizeddel későbbi visszaemlékezésében[17] ezzel ellentmondó leírást olvashatunk, az a későbbi Renner kísérlet helyszínével egyezik meg. Barnóthy Jenő, aki Eötvös halála után 5 évvel került az Intézetbe, határozottan állítja[18], hogy az Eötvös-Pekár-Fekete-kísérlet helye az épület délnyugati végében egy kis melléképület volt, ahol ma a neutron-generátor működik (5. ábra). Eötvös idejében az innen nyugatra eső épület (a C-épület) még nem állt. Délnyugati irányban alapgödröt ástak ki egy későbbi építkezés (ma az orvosegyetemi épülettömb) céljára. Kelet felöl viszont már állt a Fizikai Intézet masszív épülete, amelyen mintegy 20 méterre a kísérlet helyétől még ráadásul egy betontorony is magasodott. A mérő helyiség alatt nem volt pince, csak talaj, felette nem volt emelet. Így az Eötvös által használt laboratórium nagyon aszimmetrikus helyzetű volt környezetének tömegeihez képest: keletre és lefelé tömegek, nyugatra és felfelé semmi.

5. ábra A Fizikai Intézet épületének déli oldala
6. ábra Az épület alaprajza
25 évvel később Renner megismételte a kísérletet a geofizikai laboratóriumban, amely valószínűleg a Fizikai Intézet északi oldalán, a földszint közepén volt, ahol most a számítógépterem van. Barta György emlékezik így vissza[19] a geofizikai laboratórium elhelyezésére (R jelű szoba a 6. ábrán). Ez utóbbi helyiség alatt van pince, felette pedig egy emelet, ami azt jelenti, hogy a Renner-féle kísérlet helye (függőlegesen és kelet-nyugati irányban) már szimmetrikusabban helyezkedett el az épületben. Az Eötvös-kísérlet helyének aszimmetrikus volta újabban bizonyos jelentőségre tett szert. Talmadge és társai[20] ezzel magyarázták az Ötödik Erő jelentkezését, az összetétel-függő pozitív eredmény létrejöttét (7. ábra). A Renner-kísérlet szimmetrikus elhelyezkedése magyarázná viszont a zérus eredményt (az Ötödik Erő kikompenzálódását). A hipotétikus magyarázat akkor volna helytálló, ha az Ötödik Erő hatótávolsága 10-50 m között lenne.
7. ábra Az egyetemkert
Ezt kellene igazolnia egy újólag elvégzett
Eötvös-kísérletnek. Ahhoz azonban, hogy
ez valóban eredményes legyen, a kísérletet
végző mai fizikusoknak Eötvöstől
és munkatársaitól nemcsak a módszert,
hanem a türelmet is meg kellene tanulniuk. (Barta György
vezeti az Eötvös-kísérlet megismétlésére
irányuló munkát, szerinte a torziós
inga két egyensúlyi helyzetének leolvasása
között két napot kell várni[21].) Eötvös
az ingához a legjobb (a leglineárisabb és
a legérzékenyebben viselkedő) wolfram-szálat
használta, amelyre a méréseket megelőzően
több évig súlyt függesztettek, hogy ily
módon kiküszöböljék a zavaró
belső feszültségeket a drótból.
A kísérletek során Eötvös elvárta,
hogy munkatársai több ezer órán át
végezzenek türelmes, előítéletektől
nem befolyásolt megfigyeléseket. Az akkori helyzetet
legjobban azzal jellemezhetjük, ha elolvassuk Eötvös
"üzenetét"[5]: "A szerzők megadják
magukat az emberi sors végességének és
rábízzák az eljövendő időkre
és az eljövendő kutatókra, hogy tovább
tökéletesítsék azokat a megfigyeléseket,
melyeket ők maguk alapos tapasztalatok birtokában
is még javíthatóknak vélnek."
Az Eötvös-kísérlet mai hatása
A lehetséges nem-newtoni gravitáció iránt újabban világszerte feltámadt az érdeklődés. Hogy Fischbach és társai az Eötvös-kísérlet újragondolását kezdeményezték, az nagyban hozzájárult annak elismeréséhez, hogy Eötvös, Pekár és Fekete kísérlete gondos munka volt, amely megérdemli, hogy komolyan vegyük. A kísérlet széleskörű kedvező fogadtatásához hozzájárult, hogy a kísérletnek részletes leírása olvasható az irodalomban. Személyes beszélgetésekből a kísérlet más részleteit is megismertük ([11,18,19,21]), a kísérlet metodikájáról képet kaphattunk. A következőkben álljon itt két példa a kísérlet olyan részleteire, melyekről a szerzők nem szólnak.
A kísérletben szereplő torziós ingákat egy körülbelül egy méter oldalhosszúságú kőtalapzatra helyezték, amely mélyen a talajba volt süllyesztve. Ezekből a kőtalapzatokból néhány még ma is látható az Atomfizikai Intézetben. Az volt a feladatuk, hogy rázkódásmentes stabil helyet biztosítsanak az érzékeny ingák számára.
Ugyancsak érdekes, ahogyan az
kémiai reakcióban résztvevő reagenseket a reakció előtt és után összevetették. Mivel a reakcióban keletkezett ezüst kicsapódott a folyadékból, a reakcióban résztvevő anyagok kezdeti tömegközéppontja nem esett egybe a végtermékek tömegközéppontjával. Ha ezt az eltérést nem vették volna figyelembe, akkor lokális gravitációs gradiensek nagy (de hamis) jelet hoztak volna létre, amely az ekvivalencia elv megsértését szimulálhatta volna[10]. Valójában Eötvös és munkatársai azt találták, hogy a reagensek gyorsulása a kémiai reakció előtt és után ugyanaz, ami az elmélet alapján várható volt. Ez arra mutat, hogy a szerzők nyilvánvalóan gondosan elvégezték ennek az effektusnak a korrekcióját, bár eljárásuk részleteit nem közölték.
Öt éve volt, hogy Eötvös, Pekár és Fekete klasszikus műve egy ötödik erő lehetősége iránt érdeklődést keltett. Ezóta számos új kísérletet hajtottak végre, és sok további van még folyamatban. Az új kísérletek nem erősítették meg egy ötödik erő létezését abban a formában, amire Fischbach és munkatársai Eötvös adatai alapján gondoltak[10]. Viszont senki sem bukkant olyan hibára Eötvös kísérletében, amely a meggyőző korreláció forrása lehetne. Minthogy minden modern kísérlet eltér az eredeti Eötvös-kísérlettől, megmarad annak lehetősége, hogy van valamilyen elméleti modell, amelyben az eredeti kísérletnek egy eddig észre nem vett körülménye rejti a probléma kulcsát: Eötvösék miért láttak egy hatást, miközben az újabbak ilyent nem találnak.
Az Eötvös-kísérlet értékét mutatja, hogy továbbra is új gondolatokra ad ösztönzést. Ilyen a legújabb elképzelés, hogy az eredeti munkában a spin játszhatott szerepet[22]. Bármi lesz is az új hosszútávú erők utáni kutatás kimenetele, az Eötvös-kísérlet alapvető módon hozzájárult a természeti erők megértéséhez.
A szerzők itt szeretnék felhívni
az olvasó figyelmét arra, hogy dolgozatuk angol
nyelvű változatának (Acta Physica 69,335,1991)függelékében három, az Eötvös-kísérlettel
kapcsolatos eredeti dokumentum olvasható.
IRODALOM
[1] R. v. Eötvös, Mathematishe und Naturwissenschaftliche
Berichte aus Ungarn, 8,65,1890
[2] R. v. Eötvös, Verhandlungen der 16.
Allgemeinen Konferenz der Internationalen Erdmessung (London-Cambridge,
21-29 September 1909)
[3] R. v. Eötvös, D. Pekár, E. Fekete:
Beiträge zum Gesetz der Proportionalität von Trägheit und Gravität;
a Beneke Alapítványhoz benyújtott pályamű,1909
[4] C. Runge, Nachrichten von der Königlichen
Gesellschaft der Wissenschaften zu Göttingen, No.l, 37-41
[5] R. v. Eötvös, D. Pekár, E. Fekete,
Annalen der Physik 68, 11, 1922; A cikk angolul megtalálható:
Annales Universitatis Scientiarum Budapestiensis de Rolando Eötvös
Nominate, Sectio Geologica, 7, 111, 1963
[6] Roland Eötvös gesammelte Arbeiten,
összeállította: Selényi Pál,
Akadémiai Kiadó Budapest, 1953
[7] Renner J.: Kísérleti vizsgálatok
a tömegvonzás és tehetetlenség arányosságáról,
Matematikai és Természettudományi Értesítő,
13, 542, 1935
[8] P.G. Roll, R. Krotkov, R.H. Dicke, Annales of
Physics, New York, 26,442, 1964
[9] E. Fischbach et al., Phys. Rev. Letters, 56,
2424, 2426 1986 E. Fischbach, D. Sudarsky, A. Szafer, C. Talmadge,
S.H. Aronson, 57,1959, 1986
[10] E. Fischbach, D. Sudarsky, A. Szafer, C. Talmadge,
S.H. Aronson Annals of Physics, New York, 182,60, 1988
[11] Renner János személyes közlése
Marx Györgynek
[12] Király Péter: Az "ötödik
erő" és az Eötvös mérés,
Természet Világa, 5,154, 1987
[13] E.P. Wigner, Proc. American Philosophical Society,
93,521, 1949
[14] Fischbach E. és munkatársai, Fizikai
Szemle 38,321, 1988
[15] Király Péter: Új fejlemények
az Eötvös-kísérlet körül, Fizikai
Szemle 36,365, 1986
[16] M. Nieto, T. Goldman, R.J. Hughes: "Actually,
Eötvös did publish his results in 1910, it's just that
no one knows about it" (Los Alamos preprint, 1987)
[17] Pekár Dezső: Báró
Eötvös Loránd. Az 50 éves torziós
inga. Budapest, Kis Akadémia kiadó 1941
[18] Barnóthy Jenő személyes
közlése Marx Györgynek 1986-ban
[19] Barta György személyes közlése
Marx Györgynek 1987-ben
[20] C. Talmadge, S.H. Aronson and E. Fischbach, Progress
in Electroweak Interactions, Gif sur Yvette, 1986
[21] Barta
György személyes közlése Marx Györgynek
1990-ben
[22] A.M. Hall, H. Armbruster, E. Fischbach és
C. Talmadge, Proc. of the 2nd
Intern Conf. on Medium and High Energy Nuclear Physics, Taipei,
1990